MATH: One point, many properties
- MEEP

- Jun 27, 2020
- 2 min read

By Bruno;
You may be thinking now:"what is this point that the title is talking about?", and I'll give you a hint: it is not the centroid. Too vague? Ok... Another hint: it isn't either the circumcenter, incenter or the orthorcenter as well. No idea yet? Last hint: think of an egg!
If you are old enough, you may have already heard about Humpty-Dumpty, that british egg cartoon. But something that you probably don't know is that there are two points named after this weird character: the Humpty and the Dumpty, of course. Today, I'll only introduce you the Humpty and only a sample of its properties. Then, let's define this point.
Consider the triangle ABC in the plane. Let J be the circumference tangent to BC at B that passes through A, and let K be the circumference tangent to BC at C that passes through A. The intersection of those two circumferences is the Humpty in respect to A.
We have something like this:
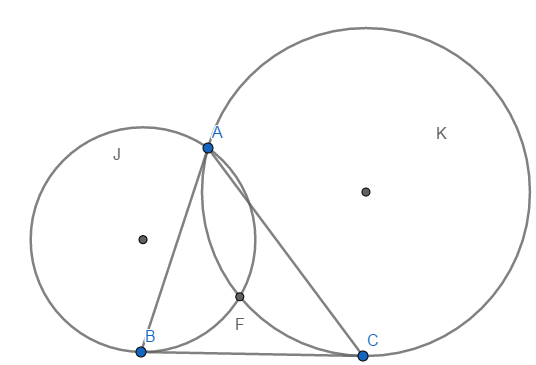
Where F is the Humpty in respect to A.
As I am lazy, I will not prove all its properties; Instead, I'll let you a .pdf attached where you can learn how to prove they.
1) The Humpty lays on the median that passes through A, where M is the middle point of BC.
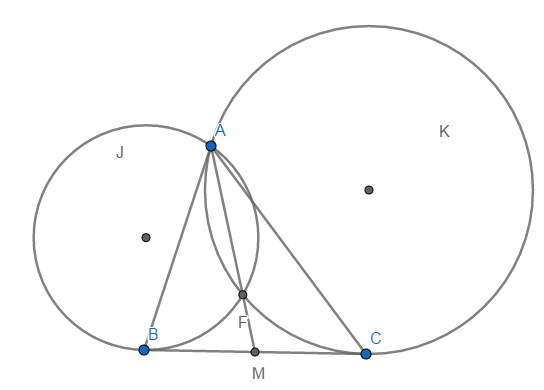
2) The reflexion of the Humpty through BC lays on the circumcircle of ABC.
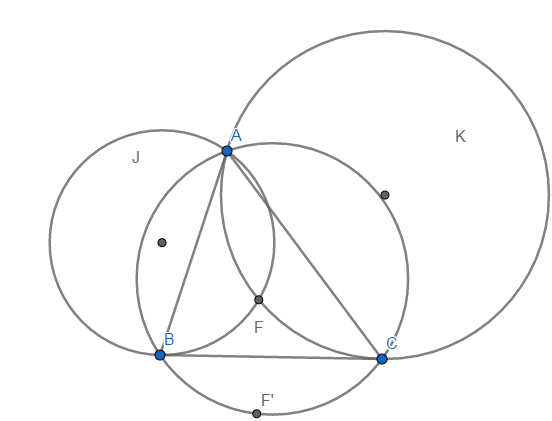
3) The angles FAC = FCB and FAB=FBC .
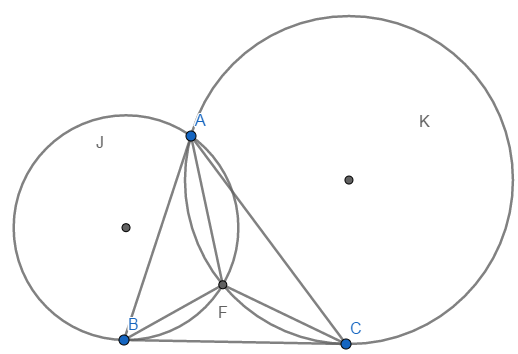
4) Let H be the orthorcenter of ABC, then the orthogonal projection of H on the median AM is the Humpty.
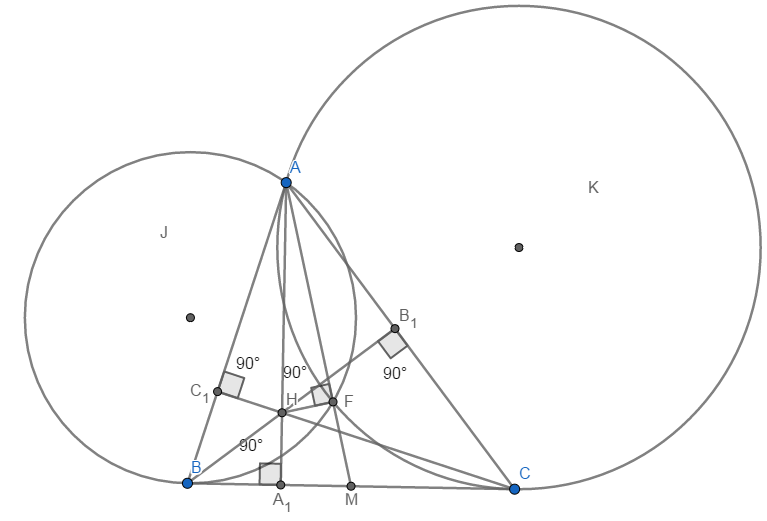
In my opinion, this last one is also the craziest among these I have listed. Of course there are a lot more properties, but you know... I am a little tired now, so I hope you have appreciated this post!
Material on the Humpty for a curious reader take a look:




Comments